[ad_1]
با مجله اینترنتی گلثمین در یک مطلب تازه از معما و تست هوش همراه باشید :

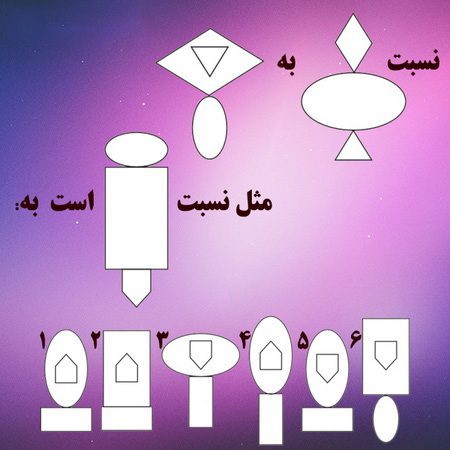
معمای ریاضی کاغذ تا شده
کاغذ مستطیل شکلی را چندین بار تا کرده ایم. در هر مرحله تا بر روی خطی موازی دو ضلع و در وسط آن ها زده شده است تا به مستطیلی با مساحت نصف مستطیل قبل برسیم. واضح است که در هر مرحله این کار به دو روش (افقی و عمودی) امکانپذیر است. در نهایت، همه تا ها را باز کرده ایم و دیده ایم در مجموع ۳۱۸ خط تای افقی و عمودی تولید شده است. کاغذ چند بار تا شده است؟
الف) ۱۳ ب) ۱۴ ج) ۱۵۹ د) ۳۱۷ ﻫ) ۳۱۸
↓↓↓
↓↓↓
↓↓↓
↓↓↓
↓↓↓
↓↓↓
↓↓↓
↓↓↓
↓↓↓
↓↓↓
↓↓↓
↓↓↓
↓↓↓
↓↓↓
پاسخ معمای المپیادی ‘کاغذ تا شده’
گزینه ب صحیح می باشد.
در صورتی که تعداد تاهای افقی و عمودی به ترتیب x و y باشد، تعداد خطوط افقی و عمودی برایر با 2x-1 و 2y-1 خواهد بود (به ازای هر خط اضافه، تعداد نواحی دو برابر می شود.) در نتیجه اگر تعداد خطوط در انتها برابر 318 باشد داریم:
2x + 2y = 320 =(101000000)2
{x,y} = {6,8}
x+y = 14
منبع:ihoosh.ir
امیدواریم از این مطلب بهره کافی را برده باشید ، بزودی با شما همراه خواهیم بود در یک مطلب تازه تر از دنیای معما و تست هوش
مجله اینترنتی گلثمین آرزوی بهترینها را برای شما دارد.